Streaming Algorithms
What are Streaming Algorithms?
They are algorithms for processing extremely large data sets where the input is presented as a sequence of items.
They can be examined in only a few passes (often just one pass), and mostly have access to limited memory.
What is Streaming?
It is maintaining compressed data on the fly, as the data is updated to apply a function F on that compressed data.
Bloom Filter (Data Structure)
Definition
It is a space-efficient probabilistic data structure. It is used to test whether an element exists in a set.
It consists of an array of bits of size "m" where each bit can be turned on/off, the number of input items equals "n", and we need a number of deterministic hash functions ("k" hash functions).
What we mean by a "deterministic hash function" is that it produces the same hashed output for the same input every time.
How It Works
We apply the "k" hash functions on the item we want to check if it exists. If at least one of the bits of the positions with indices produced by all the hash functions has a value of 0 then the item definitely doesn't exist, and if all the positions have a value of 1 then it may exist.
False positive matches are possible, but false negatives are not.
- Here is an explanation of what the last line means :
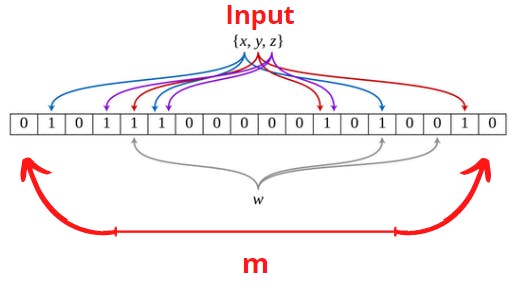
So, It means that a query returns either "Possibly in the set" or "Definitely not in the set". We can imagine a bloom filter as a hashtable.
Probabilistic Data Structures
Definition
They are data structures that provide a good approximation of the answer and a way to approximate this estimated answer.
Bloom Filter is an example of these data structures.
Advantages
Bloom filter's main advantage is not storing the elements themselves, as it stores only 1 bit for each item.
Bloom Filter Operations
Given two bloom filters with the same size and a bunch of hash functions :
- Union of two bloom filters can be implemented using bitwise OR.
- Intersection of two bloom filters can be implemented using bitwise AND.
- Insertion always succeeds.
- Deletion is not supported by default, but it can be supported using a Counting Bloom Filter.
Count-Min Sketch
As we said before a "sketch" refers to the compressed data that we can apply a function "F" on.
Count-Min Sketch has a space complexity of O(1)😯.
Count-Min Sketch is a probabilistic data structure that serves as a frequency table. It is used for computing approximately counts.
Example
What if we wanted to get the top 10 popular visited videos on youtube? We can pass on the videos and store the number of views in an array and then sort them using the QuickSort Algorithm to get the result but this may be a great effort on a huge data, so is there something better?
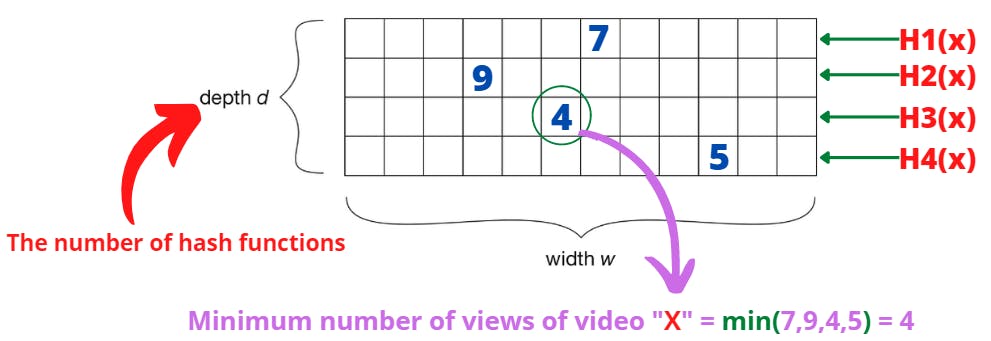
We will use a 2D-Matrix of size (d w), where "d*" is the number of the different hash functions that we would use next (the more accurate result we want, the more number of hash functions to be used).
We then apply the hash functions (H1, H2, H3,.....) on the item (video) X and for every position for the corresponding row of the hash function we increment it by 1.
- After applying all the hashing functions on the element. We get the minimum number as it sets a lower bound on the number of views of the video.
And that is why this algorithm is called a "Count-Min" algorithm.
Boyer–Moore Majority Vote Algorithm
It is used for finding the majority of a sequence of elements (or votes) using linear time O(n) and constant space O(1).
let's have an example to understand how it works.
Example
If we have "N" coloured balls (red, green, and blue) in a box. We want to know the most frequent colour among them.
We can grab two balls and if they have a different colour then we can suppose that they have never been in the box, so they cancelled each other and we repeat this operation until the majority element remains as its count will be more than the others, so at the end, we won't find another ball of another colour to cancel it with.
Implementation
class Solution {
public int majorityElement (int[] nums) {
int candidate = 0;
int count = 0;
for (int element : nums){
if (count == 0) {
candidate = element;
}
if (element == candidate) {
++count;
}else {
--count;
}
}
return candidate;
}
}
Thank you, and goodbye.